4439. Exponentiation
Find
the value of xn.
Input. Two positive integers x and n.
Output. Print the value of xn, if it does not exceed 1018.
|
Sample input |
Sample output |
|
2 10 |
1024 |
SOLUTION
exponentiation
Algorithm analysis
How to compute xn faster than O(n)? For example,
x10 = (x5)2 = (x
* x4)2 = (x * (x2)
2)2
It can be noted that x2n = (x2)n, for example x100 = (x2)50.
For odd powers, we use the formula x2n+1 = x
* x2n, for example
x11 = x
* x10.
The
following recursive formula gives us an O(log2n) solution:
![]() =
= 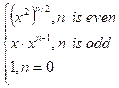
In an
iterative implementation, the case when x
= 1 and n is a large integer should be handled separately. For example, when x = 1 and n = 1018, computing xn would require 1018
iterations, which would result in a Time Limit.
Algorithm realization
The function f computes the value of xn.
long long
f(long long x, long long n)
{
if (n == 0) return 1;
if (n % 2 == 0) return
f(x * x, n / 2);
return x * f(x, n - 1);
}
The main part of the program. Read the input data.
scanf("%lld %lld",&x,&n);
Compute and print the answer
xn.
res = f(x,n);
printf("%lld\n",res);